
今回は後半にかけてちょっとややこしいですが、じっくり読んでみてください。
これが分かって弾けるようになると、ギター指板の見え方がかなり変わってきます。
インターバルを使って、ルート、メジャー3rd、パーフェクト5th(以下、略して5th)の3音からなるメジャーコード(3音からなるコードをトライアドと言います。)を、ギターの指板上で見つけていきました。
すると、いろんな場所でメジャーコードが作れることがお分かりいただけたかと思います。
前回、CメジャーのコードがCメジャーのコードたり得るための条件は、
「Cをルートとし、メジャー3rdと5thが合せて鳴らされること」
だとお伝えしました。
そのうえで、まずは3音の重なり順が、低い方からルート、メジャー3rd、5thとなる「基本形(ルートポジション)」から確認したわけですが、
この構成音のいずれかをオクターブ上にしたり、オクターブ下にしたりすることで高さの順序が変わりますね。
例)
メジャー3rdを1オクターブ下げると、低い方からメジャー3rd、ルート、5thという順序になる。
じつはコードというのは「構成音の高さの順序が入れ替わってもOK」なのです。
このあたりが、オタマジャクシの楽譜でずっと音楽をやってきた方にとっては釈然としないかもしれませんが、今回はもうそういうものだと割り切って進みましょう。
構成音の順序を入れ替える方法もいくつかありますが、今回はインバージョン(転回形)というやり方をご説明してみます。
今回も基準となる音(ルート)はCとしていますが、もちろんこれは一例にすぎません。指板上でのポジション関係はルートがなんの音であっても変わりません。
低い方からルート、メジャー3rd、5thとなっているのが基本形(ルートポジション)でしたね。
ルートを◉、メジャー3rdは③、5thは⑤で表記しています。
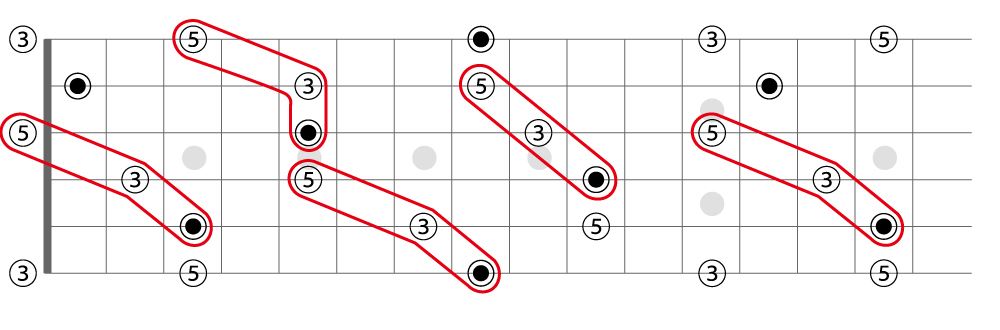
【ファーストインバージョン(第一転回形)】
基本形を元に、一番低いところにあるルートを1オクターブ上にあげると、低い方から「メジャー3rd、5th、ルート」という順になります。これをファーストインバージョンと言います。
これをギターの指板上で探していくと、こんな感じで見つけられると思います。
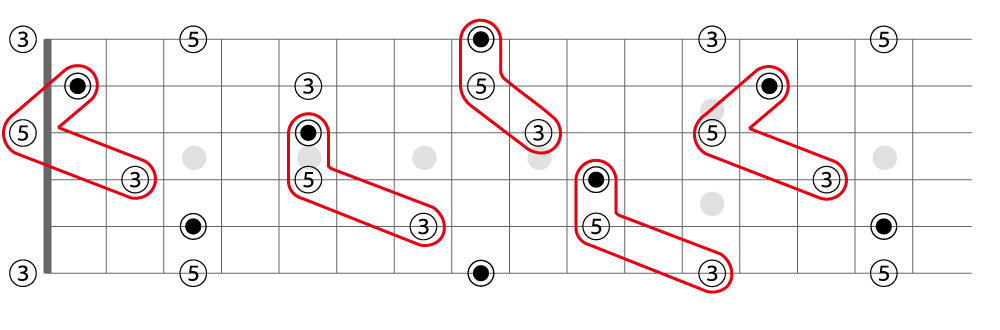
【セカンドインバージョン(第二転回形)】
同じ要領で、ファーストインバージョンの形を元に一番低いところにあるメジャー3rdを1オクターブ上にあげると、低い方から「5th、ルート、メジャー3rd」という順になります。これをセカンドインバージョンと言います。
ギターの指板上で探していくと、こんな感じ。
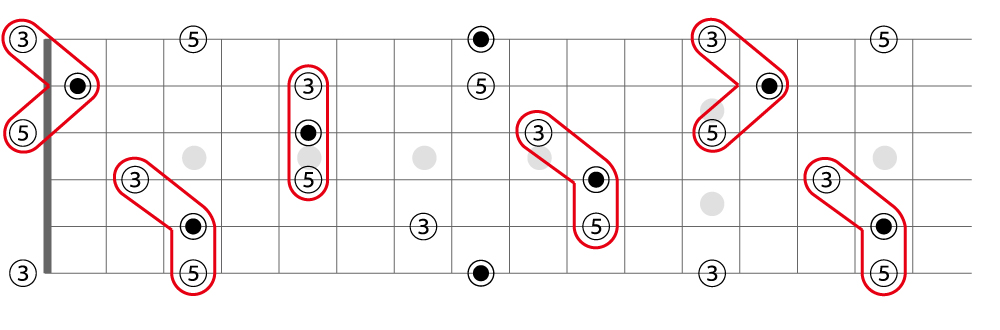
基本形と上記2つのインバージョンを合わせると、
指板上のいたるところでメジャーコードが作れる
ことになりますね!!
ただし、インバージョンで弾いたコードが、厳密に「Cメジャーコード」であるためには、1つ条件が加わります。
それは
「ルートがアンサンブルの中の一番低いところで鳴っている」
ということです。
アンサンブルの中で……とは例えば、ヴォーカル、ギター、ベース、キーボード、ドラム…といったバンド編成で演奏するとします。
Cメジャーコードを鳴らすにあたって、ベーシストがルートを低い音で弾いていれば、ギタリストやキーボーディストがファーストインバージョンもしくはセカンドインバージョンで弾いたとしても、それは純然たるCメジャーコードということになります。
「ベース音(最低音)がルート」ということですね。
お分かりでしょうか?
一方で、ギターやピアノの独奏や弾き方りなどにおいては、構成音の順序を入れ替えたことによりベース音(最低音)がルート以外の音になっていたとすると、それは厳密に言えば別の名前のコードになってしまうわけです。
Cメジャーコードの構成音を音名で表すと
ルート=C メジャー3rd=E 5th=G
となります。
これがファーストインバージョンでは「E、G、C」という順序になるわけで、
これを正式なコードネームで言うならば、「C/E(E分のCと読む)」もしくは「ConE」となります。
同様にセカンドインバージョンでは「G、C、E」という順序になり、コードネームは「C/G」もしくは「ConG」となります。
これらは「分数コード」および「オンコード」と呼ばれます。
分数の場合は一番低い音(ベース音)が分母となり、分子には構成音からなる(元の)コードが示され、オンコードの場合はそのままの英語の解釈で、Cというコードが◯というベース音に乗っかっている、という意味です。
バンドなどのアンサンブルでも、あえてベーシストがルート以外の3rdや5thをベース音として弾き、全体として分数コード(オンコード)の響きを作ることもあります。
※ちなみに分数で表すコードにはもう1つ別の捉え方もあります。
アッパーストラクチャーという「コードの上にコードが乗っかっている(2つのコードが重なっている)」状態がありまして、それを分数を使って表します。
とりあえずは、分数はオンコードとは違う使い方をすることがある、くらいに覚えておいてください。
つづきます。
