はい、音楽理論講座の4回目です。

前回は、一般的に気持ちが良いとされている響きと、そうでない響きとはどんなものか、聴きながら確かめてみました。

これが「一般的に」と言えるのは、多くの人に聞いて回ったというデータがあるわけではなく（あるかもしれませんが）、いちおう根拠があります。

それは周波数の比率です。

音というのは、物理的には空気の振動なんですよね。

物を叩いたり、弾いたり、擦ったりすると空気が震えるわけです。

その震えが一定時間の内で何回繰り返されるか、によって音の高さが決まります。

それを数値化したものを周波数と言います。（単位はHz（ヘルツ）を使います。）

※専門外ですので、雑な説明でスミマセン。

で、基準とした音の周波数ともう1つの音の周波数の比率を見ていくとですね……。

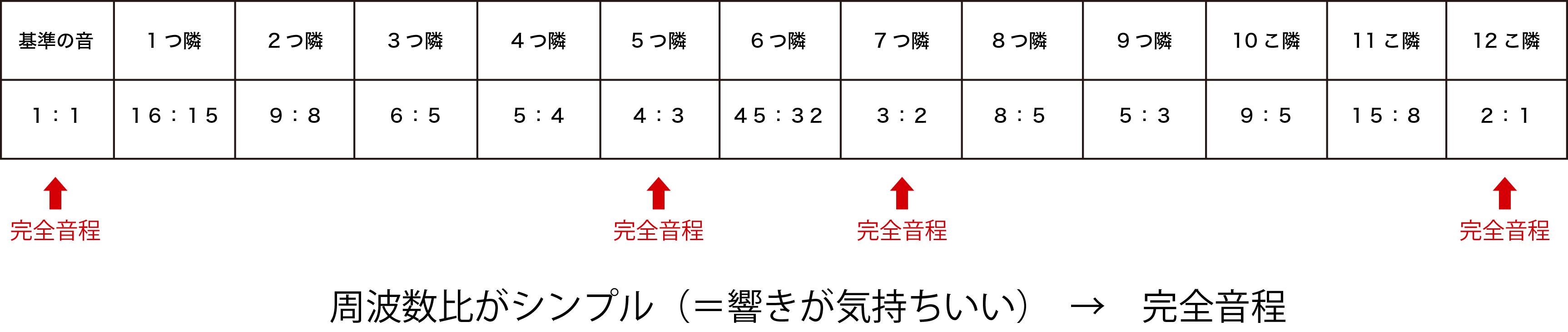
前回の最後に確認した、「12こ隣」の場合、2：1になるんですね。

基準音が1回波うつ時間で、もう1つの音はちょうど2回波うつことになります。

これ、とってもシンプルですよね。分かりやすい。

それに対して、不協和とされていると紹介した「6つ隣」の場合……45：32だそうで。

……もうなんだか分かんない比率ですね。

その要領でいくと、前回確認した響きの周波数比はそれぞれ

1つ隣が、16：15

2つ隣が、9：8

4つ隣が、5：4

7つ隣が、3：2

となります。

つまり、気持ちいいとされている響き合いは周波数比がシンプルで、気持ちよくないとされている響き合いは周波数比が複雑だということなんですね。

以下が12こ隣までを半音ごとに並べた表です。

【純正律と平均律】

いちおう補足です。

「だいたいそういうことなんだ」と思っておいていただければいいのですが、正確に言うと上記の表にある周波数比は、純正律というやつのものです。

1：1（基準音）から2：1（鍵盤で12こ隣）までの間を、基準の音との周波数比をなるべくシンプルにしつつ、12に区切っていったものになります。

なるべくシンプルに、ってことなので、それで得られる響きは気持ちの良いものとされています。

ですが、これによってできる区切りを低い方から順番に並べたもの（半音階ということになります。）は1段毎の高さがまちまちになってしまうんだそうです。算数に強い方は確認してみてください。半音、と言っても全てが同じ音程ではなくなってしまうと。

のちにお話ししますが、音楽には転調や移調なるものがあります。

純正律は、1つのキー（調）で演奏される分には純度の高い響きを得られますが、半音のステップがまちまちであるために転調や移調ができません。

ですので、現在は、とくにポピュラーミュージックにおいては純正律は使われないのが一般的です。

代わりに、1：1（基準音）から2：1（鍵盤で12個隣）までの間を均等に12分割した、つまり全ての半音が同じ音程になる、平均律が用いられています。

で、平均律においては、周波数比は上の表よりもどうしても複雑になってしまいます。

でも「近似値としては許容範囲だとして、転調や移調ができることを優先しよう」てことみたいです。

ということで、純正律と平均律はまったく違うものですが、ここでは分かりやすさを優先して、平均律でありながら純正律の周波数比表を用いています。

こだわる人からは当然の異論があるでしょうが、この講座の対象としている方はあまり気にしなくていいんじゃないかと思っています。

————————-

はい。で、話を戻すと、いちおう響きが気持ちがいいか否かの物理的な理由もなんとなくある、ということですね。

次にこの1つ1つに名前をつけていきます。

響きの確認でとくに気持ちが良いとされているものを、完全音程と言います。

この中では、

1：1（つまり基準音とまったく同じ高さの音）

4：3（5つ隣）

3：2（7つ隣）

2：1（12個隣）

が、それにあたります。

つづきます。