はい、音楽理論講座の5回目です。
基準の音ともう1つの音との響きを半音ごとに確認して、それに名前をつけていきます。
1:1(つまり基準音とまったく同じ高さの音)
4:3(5つ隣)
3:2(7つ隣)
2:1(12こ隣)
これらを完全音程と呼びます。
ということはですね、それ以外は不完全だということです。
と、ここで歴史を紐解いてみますと、みなさんがご存知の「ドレミファソラシ」なるものを最初に発見・提唱したのは、かのピタゴラスだとされています。ピタゴラスイッチのピタゴラス。
紀元前6世紀とかの大昔のことだそうです。
ただし、この時点では「ドレミファソラシ」と言った名前はまだなかったようです。「ドレミ」は、11世紀にイタリアの修道士グイード・ダレッツォという人が、キリスト教の聖歌「ヨハネ賛歌」のひと節ずつの頭文字から考案したそうです。
さて、ピタゴラさんは、響きの気持ちいい、つまり周波数比のシンプルな3:2に目をつけて、ある音①と周波数比が3:2である音②を見つけ、今度は②を基準にまた周波数比が3:2になる音③を見つけ、さらに③を基準に周波数比が3:2になる音④を見つけ……。という要領の繰返しで、ずーーーっと後に「ドレミファソラシ」と名付けられる音高の区切り目というか、関係性を作り(見つけ)ます。
ただ前述したように、これにはまだ「ドレミ…」といった名前がつけられていませんでした。この関係性の中での1つ1つの音がなんと呼ばれていたか、じつは分かりません。私が不勉強なだけかもしれませんが。
とにかく「ドレミ」でも「CDE」でもなかったとすると、考えられるのは……そうですね。「数字」ですね。
ピタゴラスっていう人は数学者ですもんね。
数字でいきましょう!
周波数比が1:1のところが「1」
周波数比が2:1のところが「8」
その間を埋めて、1, 2, 3, 4, 5, 6, 7, 8, とナンバリングします。
みなさん「オクターブ」という言葉を聞いたことありませんか?
もしくは普通に使っている言葉かもしれませんね。
「オクタ」ってのはギリシャ数字の「8」なんですよね。
てことで、周波数比が2:1の関係を「オクターブ」と言います。
日本語では、数字に「度」とつけて、さらに前回の最後にお話しした「完全」もつけて…
「完全8度」と言います。
その要領で、
周波数比が1:1の関係を「ユニゾン」または「完全1度」と言います。
同様に周波数比のシンプルな完全音程は
周波数比が4:3の関係を「パーフェクト4th / 完全4度」
周波数比が3:2の関係を「パーフェクト5th / 完全5度」
と言います。
残りの 2, 3, 6, 7, は、前回の表に当てはめると、
「2」は、周波数比が9:8の関係(2つ隣)
「3」は、周波数比が4:3の関係(5つ隣)
「6」は、周波数比が5:3の関係(9つ隣)
「7」は、周波数比が15:8の関係(11こ隣)
となります。
(※実際には、ピタゴラスの作った音律の周波数比は、純正律とも平均律とも微妙に違います。前回お話ししたとおりこの講座の中では、分かりやすさを優先し、それぞれの微妙な違いを許容範囲としていきます。)
ここまでを表で確認してみてください。

見てみると、ナンバリングした「2, 3, 6, 7」の左側は、まだ名前がつけられておらず空欄のままですね。
ここを小数点を使って「1.5」や「2.5」としていく手もあったでしょうが、音楽理論では「メジャー/マイナー」もしくは日本語で「長/短」という表現を使います。
先に紹介した「2, 3, 6, 7」をそれぞれメジャー2nd(長2度)、メジャー3rd(長3度)、メジャー6th(長6度)、メジャー7th(長7度)とし、それぞれの左側の空欄だったところは、マイナー2nd(短2度)、マイナー3rd(短3度)、マイナー6th(短6度)、マイナー7th(短7度)とします。
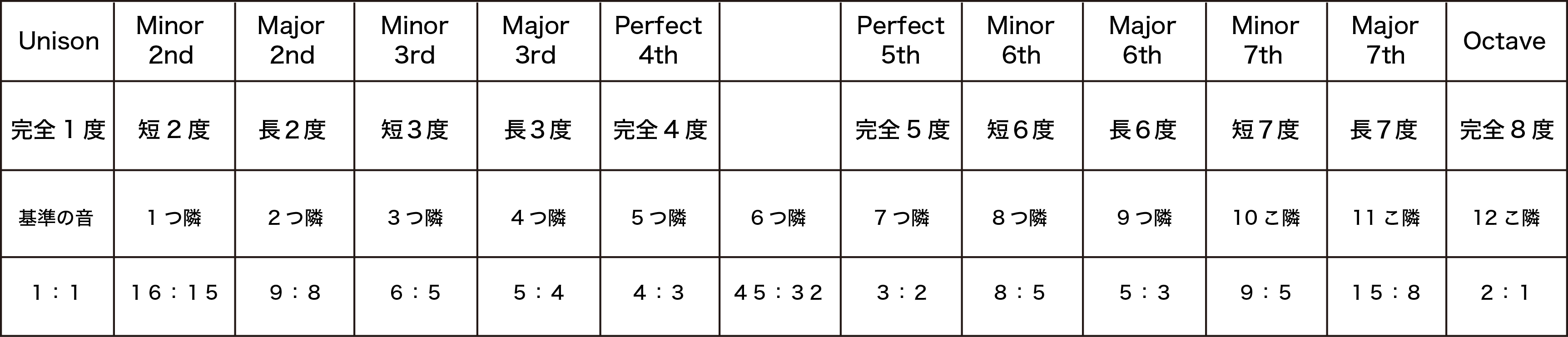
あと1ヶ所空欄がありますが、長くなったのでここまでです。
つづきます~~。
